문제 링크 : https://www.acmicpc.net/problem/17136
문제 설명
<그림 1>과 같이 정사각형 모양을 한 다섯 종류의 색종이가 있다. 색종이의 크기는 1×1, 2×2, 3×3, 4×4, 5×5로 총 다섯 종류가 있으며, 각 종류의 색종이는 5개씩 가지고 있다.
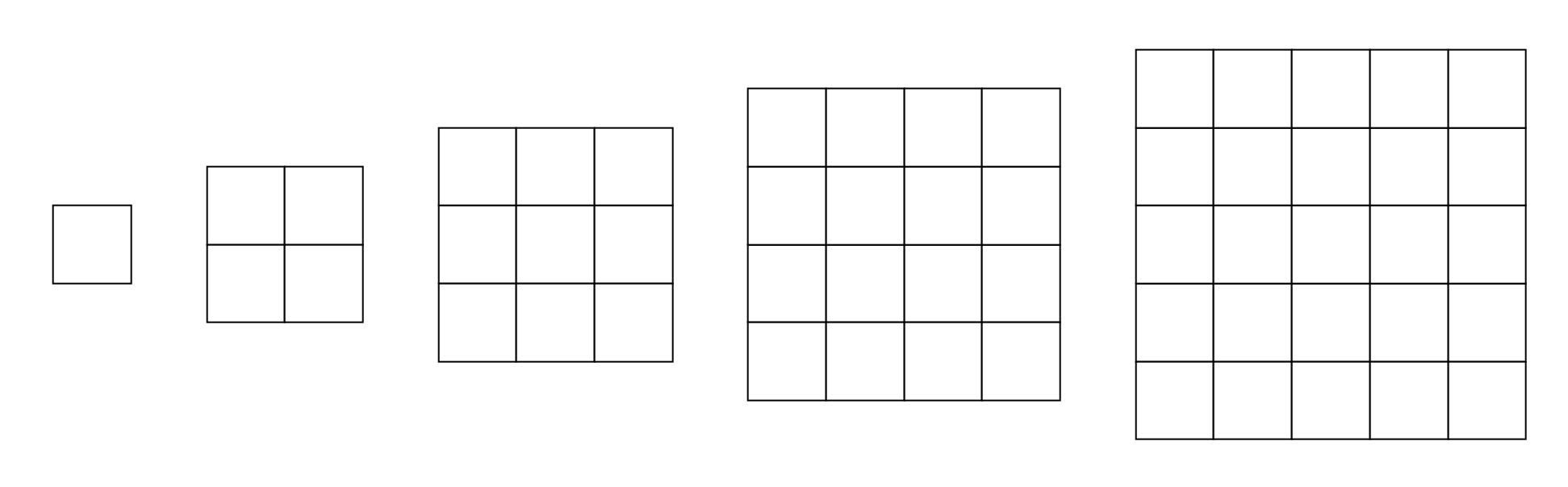
<그림 1>
색종이를 크기가 10×10인 종이 위에 붙이려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 0 또는 1이 적혀 있다. 1이 적힌 칸은 모두 색종이로 덮여져야 한다. 색종이를 붙일 때는 종이의 경계 밖으로 나가서는 안되고, 겹쳐도 안 된다. 또, 칸의 경계와 일치하게 붙여야 한다. 0이 적힌 칸에는 색종이가 있으면 안 된다.
종이가 주어졌을 때, 1이 적힌 모든 칸을 붙이는데 필요한 색종이의 최소 개수를 구해보자.
제한사항
- 모든 1을 덮는데 필요한 색종이의 최소 개수를 출력한다.
- 1을 모두 덮는 것이 불가능한 경우에는 -1을 출력한다.
풀이 순서
- 가장 큰 색종이부터 시작해서 작은 색종이로 채우는 경우 까지 모든 경우의 수 중 색종이를 가장 적게 사용하는 경우 탐색
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class boj_17136 {
static int SIZE = 10;
static int[][] map;
static int ans = Integer.MAX_VALUE;
static int[] color = {0, 5, 5, 5, 5, 5};
public static void main(String[] args) throws IOException {
map = new int[SIZE][SIZE];
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
for (int i = 0; i < SIZE; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < SIZE; j++) {
int val = Integer.parseInt(st.nextToken());
map[i][j] = val;
}
}
dfs(0, 0);
System.out.println(ans == Integer.MAX_VALUE ? -1 : ans);
}
static void dfs(int idx, int cnt) {
if (idx == 100) {
ans = Math.min(ans, cnt);
return;
}
if (ans <= cnt) {
return;
}
int y = idx / 10;
int x = idx % 10;
if (map[y][x] == 1) {
for (int start = 5; start > 0; start--) {
if (color[start] > 0) {
if (check(y, x, start)) {
fill(y, x, start, 0);
color[start] -= 1;
dfs(idx + 1, cnt + 1);
fill(y, x, start, 1);
color[start] += 1;
}
}
}
} else {
dfs(idx + 1, cnt);
}
}
static boolean check(int y, int x, int size) {
if ((y + size) <= SIZE && (x + size) <= SIZE) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
if (map[y + i][x + j] != 1) {
return false;
}
}
}
return true;
}
return false;
}
static void fill(int y, int x, int size, int state) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
map[y + i][x + j] = state;
}
}
}
static void debug(int idx) {
System.out.println("---" + idx);
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
System.out.println("------------");
}
}
후기(틀렸던 문제) : 가장 큰 색종이부터 작은색종이로 내려오는 로직은 맞았지만, 모든 경우의 수를 탐색하진 않았다. 때로는 작은 색종이로 빈틈없이 채우는 것이 더 적은 색종이를 사용할 수 있음, DFS + 백트래킹의 대표적인 문제였다
'Algorithm' 카테고리의 다른 글
| [프로그래머스 - BFS/DFS] 네트워크 (0) | 2020.01.28 |
|---|---|
| [프로그래머스 - 힙(Heap)] 디스크 컨트롤러 (0) | 2020.01.28 |
| [프로그래머스 - 정렬] H-Index (0) | 2020.01.27 |
| [프로그래머스 - 정렬] 가장 큰수 (0) | 2020.01.27 |
| [프로그래머스 - 스택/큐] 다리를지나는트럭 (0) | 2020.01.27 |